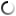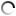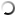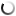 loading
loading
Arts & CultureObject lessonMove over, Pythagoras Ulla Kasten is associate curator of the Yale Babylonian Collection.
 Mark MorosseThese clay school tablets from Yale's Babylonian Collection show that students in Mesopotamia learned about pi and the square root of 2, and wrote them in base-60 cuneiform. View full imageGeometry students everywhere learn the formula for calculating the hypotenuse of a right triangle as the “Pythagorean theorem.” But a well-preserved clay tablet in Yale’s Babylonian collection shows that Mesopotamian students were crunching their own version of a2+b2=c2 more than a thousand years before the Greek philosopher Pythagoras was born. The tablet (center) is one of several in Yale’s collection from the Old Babylonian Period, ca. 1800–1600 BCE, that illustrate how students in scribal schools learned much of what we now think of as Greek geometry. (At left is a tablet showing how to find the area of a trapezoid; at right is the formula for calculating the area of a circle—including a rough approximation of pi.) Several hundred such mathematical tablets are known. They were used as teaching aids in schools: the teacher would write the formula in cuneiform script on the front of the wet clay tablet, and the student was supposed to copy it on the back. Other mathematical tablets contain Babylonian versions of today’s dreaded “word problem”—asking students to calculate the weights of stones or the number of bricks needed to build a wall. (Thankfully for Babylonian students, there were no trains leaving Pittsburgh at 4 p.m. yet.) Most of the school tablets were likely recycled back into the classroom clay bin. The Babylonians expressed mathematical concepts using a different numerical system from that of their Western heirs: a simple positional notation system with base 60. (We still use the sexagesimal system, for example in measuring time and the degrees around a circle.) Any number could be represented with combinations of just two symbols: there was a sign for 1, which was repeated for single-digit numbers from two through nine, and a sign for 10. When the total reached 60, the Babylonians would repeat the symbol for 1, and start counting again. The tablet with the pre-Pythagorean formula has a drawing of a square with its diagonals. Just outside the square, at its upper left side, are small characters giving the length of one side. The long number written along the diagonal is the square root of 2. Just below that is the length of the diagonal. Students could solve for the length of the diagonal by multiplying the length of one side by the square root of 2, just as geometers do now. It is not known whether the Greeks developed geometry independently of the Babylonians or simply picked it up from their trading partners. Maritime trade in the Mediterranean, as well as overland trade routes through Anatolia and Syria to Mesopotamia and beyond, existed already in the second millennium BCE. The Greeks’ reliance on the Babylonian base-60 system for describing arcs and circles suggests that they may have learned geometry abroad. The Babylonians are slowly regaining the credit for discovering these mathematical concepts. The Yale “Pythagorean” tablet—the best-known tablet in Yale’s collection—has been published in math textbooks around the world.
The comment period has expired.
|
|